ist im Oktober 2013 in der Reihe Springer-Lehrbuch Masterclass erschienen, 396 S., über 300 Abb., davon etwa 80 Abb. in Farbe, ISBN 978-3-642-37937-6
Das Lehrbuch bietet dem Leser sowohl eine Einführung in die mathematische Darstellung neuronaler Strukturen, als auch in die sich aus einigen dieser Strukturen zusammensetzenden Assoziativmaschinen.
Zur Unterstützung der Leser sind allen Kapiteln Übungsaufgaben angefügt, deren Lösungen sich im Anhang des Buches befinden. Ferner steht der Assoziativ- maschinen-Simulator VidAs zur Verfügung, mit dem man die Programmierung der beispiel- gebenden Assoziativmaschine System 9 einüben kann. Zur Erläuterung der neuromathe- matischen Zusammenhänge und zur Übung wird das Computer- algebrasystem Maxima genutzt.
Prof. Dr. rer. nat. habil. Hans-Joachim Bentz hatte von 1990 bis 2012 den Lehrstuhl für Angewandte Mathematik an der Universität Hildesheim mit den Forschungs-gebieten Neuromathematik, Diskrete Strukturen und Stochastik inne.
Dr. rer. nat. Andreas Dierks war mit den Fächern Mathematik, Physik und Informatik seit 1980 in der Lehre an Schule und Hochschule tätig und ist in der Forschung mit Neuromathematik und Assoziativmaschinen befasst.
Grundlegendes
Die Leistungen eines Computers werden durch Prozessoren erbracht, die als programmierbare Rechenwerke zu verstehen sind. Demgegenüber ist eine Assoziativmaschine (AM) – auch Matrixprozessor genannt – eine völlig neue Art Prozessor, die sich als Alternative und mit Vorteilen ebenfalls zum Aufbau oder zur Ergänzung von Computern eignet. Die Architektur einer AM wird durch Assoziierwerke gebildet und unterscheidet sich damit fundamental von Von-Neumann-Rechnern, die um ein Rechenwerk herum aufgebaut sind. Als Assoziierwerke werden vornehmlich matrixförmige Assoziativspeicher eingesetzt, die Assoziativmatrizen. Diese Assoziativspeicher dienen der AM als Programm- und als Datenspeicher, so dass das Prozessorsystem sowohl hinsichtlich der Ausführung von Programmen als auch bezüglich des Zugriffs auf ihre Datenspeicher störunanfällig und fehlertolerant wird.Aufgrund des Einsatzes von Assoziierwerken ergeben sich für die Programmierung von AM Besonderheiten. Diese sind Gegenstand der Assoziativen Programmierung. Die AM wird damit zu einem frei programmierbaren Prozessor.
Auch wenn sich in einer AM kein Rechenwerk befindet, so kann man ihr dennoch das Rechnen beibringen. Mit der Beschreibung der dazu nötigen Abläufe beschäftigt sich das Assoziative Rechnen.
System 9
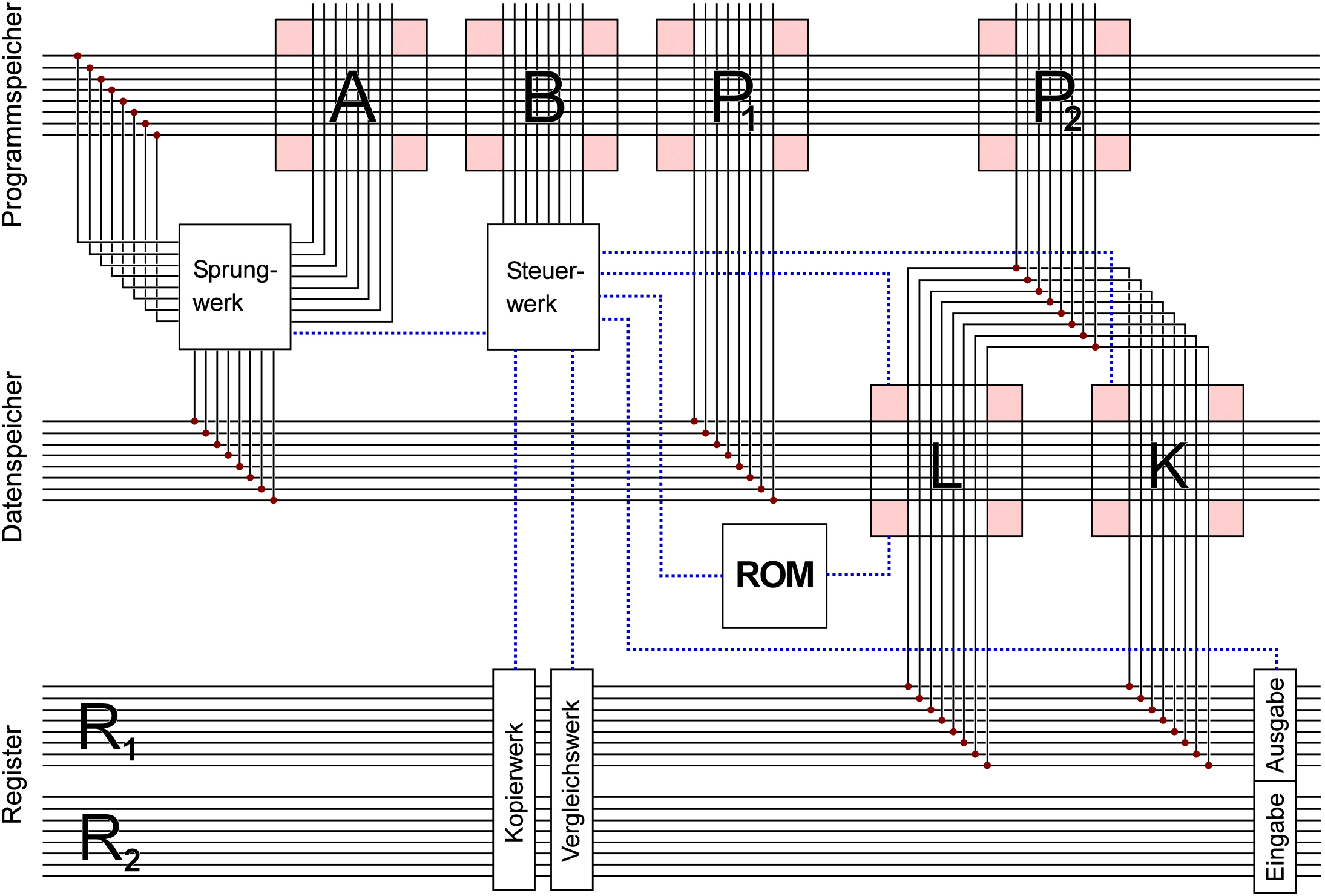Die Assoziativmaschine System 9 wird aus sechs Assoziativmatrizen aufgebaut, wovon vier den Programmspeicher (A, B, P1, P2) und zwei den Datenspeicher (L, K) bilden. Dabei stellt L das "Langzeitgedächtnis" und K das "Kurzzeitgedächtnis" dar. Es sind viele andere Aufbauten von Assoziativmaschinen möglich, unter anderem durch den Einsatz von assoziativen Quadern.
VidAs 5
Die Programmierung der Assoziativmaschine System 9 kann durch die Simulationssoftware VidAs 5 untersucht werden. Die aktuelle Version des Simulators kann hier heruntergeladen werden.The basics
An associative machine (matrix processor) consists of several associative memories instead of being composed by arithmetic logic units like a Von-Neumann-processor. For this purpose mainly associative matrices are used as associative memories. This kind of associative memory serves as a memory for programs as well as a memory for data. Therefore the fault-tolerant characteristics of associative matrices are transmitted to the associative machines and they become insusceptible to errors.Because of the use of associative memories we have to choose other programming paradigms than the well-known ones taken for Von-Neumann-computers. These paradigms are summed up in the methods of the associative programming. In this way the associative machine becomes a freely programmable machine.
Although an associative machine has no arithmetic logic unit we might teach arithmetic skills to it by the concepts of the associative computation.
System 9
The associative machine which is called System 9 is formed by six associative matrices. Four of them (A, B, P1, P2) store the programs and the others (K, L) the data. K might be understood as the short term memory and L as the long term memory. Many other forms of associative machines are possible for example by using associative cuboids.
